Fixed point sqrt and rsqrt approximations
05 Mar 2017
Binary fixed-point real number representation is a popular alternative to floating point. It is useful on embedded systems without native float support, or in situations where uniform precision across the whole representable range is preferred.
The main idea is to store an approximation of a real number as some integer value equal to the real number scaled by 2N, there N is a number of fractional bits. For example 9.34375 with 8 fractional bits will be stored as 9.34375*256 = 2392 = 0x958. Alternatively, this can be written as I·2E, where I is an integer and E is an exponent (usually negative): 2392*2-8 = 9.34375.
Basic arithmetic operations can be expressed with integer arithmetic: addition and subtraction work as is, multiplication require additional division of the product by 2-E and division require scaling the dividend by 2-E. And all those additional operations with 2-E can be performed as a combination of bit shifts, additions, and subtractions.
So basic operations are simple and fast. But how can we calculate more complex functions? For example sqrt(x) and 1/sqrt(x)?
Here is my single-header C++ fixed-point math library with sqrt and rsqrt approximations. Next, I will describe how this calculation is performed.
Sqrt
We want to find a value of y from y2 = x.
Let's use Newton's method to find a root of the function f(y) = y2 - x.
Derivative of this function is f'(y) = 2y.
And starting with some initial guess of y we can iteratively calculate
yi+1 = yi - f(yi)/f'(yi) = (yi - x/yi)/2
What value can be used as a good initial guess?
Our real number x is represented as I·2E.
sqrt(x) = sqrt(I·2E) = sqrt(I·22E·2-E) = sqrt(I·2-E)·2E
So we need to calculate new integer representation as close to sqrt(I·2-E) as possible.
Let's look at the List of logarithmic identities and do some math:
log(sqrt(I·2-E)) = log(I·2-E)/2 = (log(I)+log(2-E))/2
And for binary logarithm this turns into:
log2(sqrt(I·2-E)) = (log2(I) - E)/2
So full equation for a new integer represenattion is:
sqrt(I·2-E) = 2(log2(I) - E)/2
The integer part of the binary logarithm can be quickly calculated with CLZ/BSR (count leading zeros/bit scan reverse) instructions.
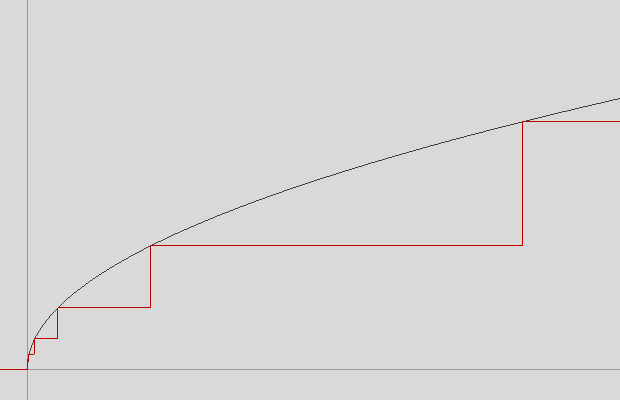
Here is a plot of such sqrt guess d = 2(int[log2(I)] - E)/2:
Click image to open a graph in the GLSL graph WebGL 2 app
Nice stairs which we can improve by linear interpolation:
Each level d starts at x = d2 and ends at x = 4d2 where it goes up to 2d.
Linear ramp function will be:
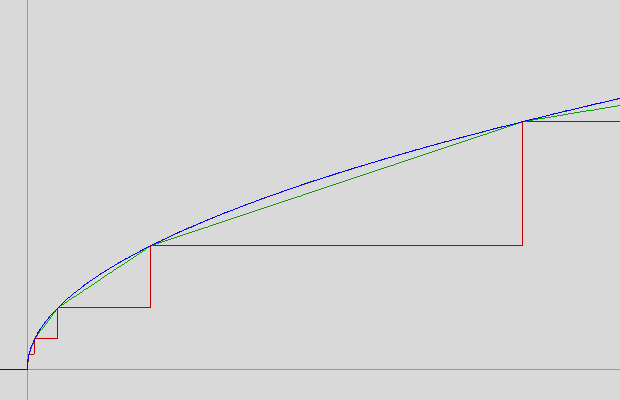
d + (x-d2)·(2d-d)/(4d2-d2) = (x/d + 2d)/3
Finally, we can apply Newton's method and get our approximation:
Click image to open a graph in the GLSL graph WebGL 2 app
This method of calculation of sqrt requires one integer division for initial guess and one division for each Newton iteration. All other divisions are by constants and are optimized by shifts and additions/subtractions. For graphics programming 1/sqrt(x) function is usually more useful then sqrt. And because integer divisions are slow so calculation of 1/sqrt(x) with actual fixed-point division can be expensive. Let's see if there is a faster method.
Rsqrt
Newton's method again, we need root of f(y) = 1/y2 - x
Derivative is f'(y) = -2/y3
And iterative approximation of rsqrt is:
yi+1 = yi - f(yi)/f'(yi) = yi·(3 - xyi2)/2
Notice what there are no 'real' divisions here!
Initial guess for rsqrt
Substitute I·2E as x:
1/sqrt(I·2E) = (2-E/sqrt(I·2E))·2E = sqrt(2-3E/I)·2E
So we need to find a new integer representation close to sqrt(2-3E/I). Again, with some logarithm math:
log2(sqrt(2-3E/I)) = (-3E - log2(I))/2
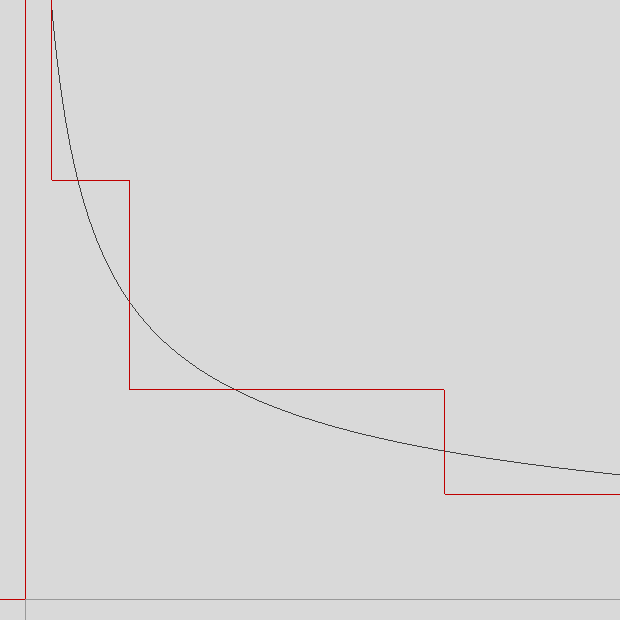
And with integer part of log2(I) our approximation d = 2(-3E - int[log2(I)])/2:
Click image to open a graph in the GLSL graph WebGL 2 app
Each level d here starts at x = 0.5/d2, there rsqrt(0.5/d2) = d·sqrt(2), then d crosses rsqrt(x) at x = 1/d2 and continues to x = 2/d2, there it drops down to the next level 0.5·d. We can approximate our function here as a maximum of two linear functions:
f1 = d + (x-1/d2)·(d-d·sqrt(2))/(0.5/d2)
f2 = d + (x-1/d2)·(d·sqrt(2)/2-d)/(1/d2)
And after some simplification:
max(f1,f2) =
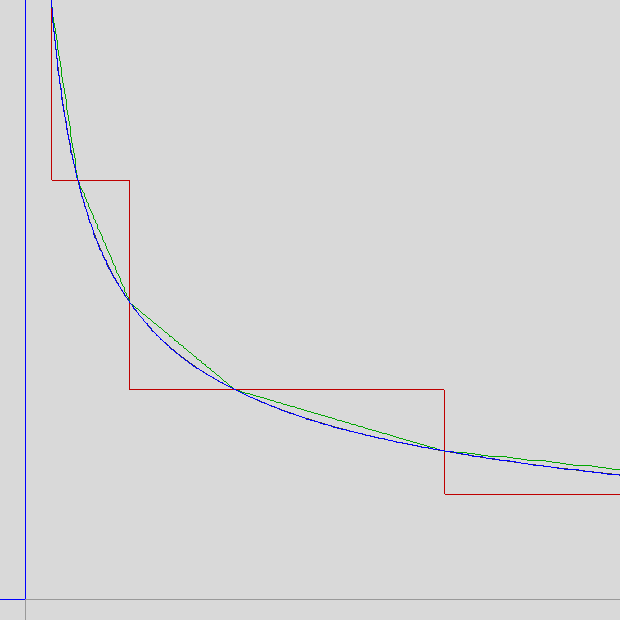
d+d·max((xd2-1)·(2-2·sqrt(2)),(xd2-1)·(sqrt(2)/2-1))
No divisions here too!
And with a single Newton's method iteration:
Click image to open a graph in the GLSL graph WebGL 2 app
Sqrt without divisions
With Goldschmidt’s algorithm and our initial guess for 1/sqrt it is possible to calculate both sqrt and 1/sqrt without divisions:
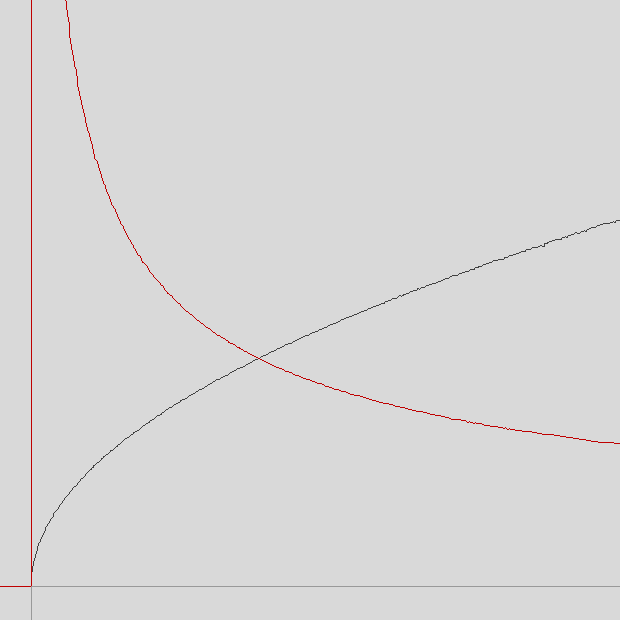
Click image to open a graph in the GLSL graph WebGL 2 app